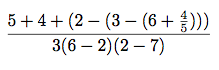SICPをやる記録 その2 1.1〜1.1.6

SICP計算機プログラムの構造と解釈 第二版
1.1〜1.1.6までの学習記録。

• 基本式 言語が関る最も単純なものを表す.
• 組合せ法 より単純なものから合成物を作る.
• 抽象化法 合成物に名をつけ, 単一のものとして扱う.

数を表現する式は 基本的な手続き(+や*など)を表現する式と組み合せて合成式とし, 数に対するそれらの手続きの作用を表現することが出来る. 例えば:

(+ 137 349)
486

これがSchemeの文法か

式の並びを かっこで囲んで 手続きの作用を表現する上のような式を組合せ (combinations)という. 並びの左端の要素を 演算子(operator), 他の要素を 被演算子(operands)という. 組合せの 値は演算子が指定する手続きを, 被演算子の値である 引数(arguments)に作用させて得る.

オペレーター、オペランドね

define で名前をつける（変数）
(define hoge 5)
で、解釈系はhogeと5を対応付ける。

値と記号を対応づけ, 後にそれが取り出せるためには, 解釈系は名前とオブジェクトの対を見失わないための, 何か記憶を保持していることに他ならないことは明らかである. この記憶を 環境(environment)(より正確には, 後になって計算は多くの異る環境に関るということが分る故に 大域環境(global environment))という.

グローバル！

評価の規則は, 本質的に 再帰的(recursive)である; つまり, 手順の一部に規則自身を呼び起す必要がある.

ある組み合わせの評価を完了させるには、組み合わせの各要素の評価を行わなくてはいけない。
組み合わせの要素をノードとし、組み合わせをツリーとする。
各ツリーのルートをノードとし、組み合わせ全体を一つのツリーとして表現する。

上の評価規則が定義は扱わないことに注意して欲しい. 例えば, (define x 3) の評価はdefineを二つの引数(一方は記号xの値で, もう一方は3)に作用させるのではない. defineの目的はxを値に対応づけることでしかない. (つまり, (define x 3)は組合せではない.)

defineは特殊形式であって、組み合わせではない。すなわち評価をすべきものではない。

一様な形に書けるのに, ただ便利ということで, 別の形をとる表層構文をPeter Landinの作った用語で構文シュガー(syntactic sugar)という。

言語によってこのあたりの考え方は違うのでしょうねえ...Pythonは同じことをやるのにはひとつのコード、という考え方ですし

さらに強力な抽象化技法である 手続き定義(procedure definitions)を学ぼう. これにより, 合成演算に名前を対応づけ, 一体として指すことが出来る.

関数ということでよいのかな？
手続き＝プロシージャ　ということか。プロシージャってなんだか言いにくいから、こんどプロシージャって出てきたら脳内で変換しておこう

(define (⟨name⟩ ⟨formal parameters⟩) ⟨body⟩)

name が合成手続きの名前、formal parametersが引数、bodyが値を評価するための式。bodyの中ではformal parametersが使われているが、
実際の呼び出しの際にはこのformal parametersが実際の引数と差し替えられて評価される。

例えば引数を二倍にして返す合成手続きdoubleは、
(define (double x) (* x 2))
で定義できる。

また、この合成手続きを使った合成手続きを定義することもできる。
5x^2 + 3y^2
を返す合成手続きを作る時、
まず
(define (square x) (* x x))
を定義し、
さらに
(define (nijishiki x y)(+ (* (square x) 5) (* (square y) 3)))
を定義すれば、

(nijishiki 2 3)
47

と合成手続きを使った合成手続きが定義できる。合成手続きは、基本手続き（+や*など、もともと用意されている手続き）と同じように使える。

合成手続きを引数に作用させるには, 各仮パラメタを対応する引数で取り替え, 手続きの本体を評価する.

評価する、というのは、要素の各組み合わせを評価し、結果をまた組み合わせとして評価し...を評価する必要がないところまで繰り返すこと。

置換えの目的は, われわれが手続き作用を考える時の補助であって, 解釈系の実際の働きを述べるものではない. 解釈系は仮パラメタに値を置き換えて, 手続きの字面を操作しつつ手続き作用を評価するのではない. 実際には, 「置換え」は, 仮パラメタの局所環境を使って実現している.

解釈系は引数をformal parametersと置き換えた後、評価しているのではない。

解釈系が評価を行うにあたって、その順序には種類がある。
作用的順序の評価(applicative-order evaluation)：手続きに与えられた引数をformat parametersに置き換え、部分の組み合わせから評価する
正規順序の評価 (normal-order evaluation)：基本的演算子だけを持つ式が出てくるまで引数の置き換えは行わない

場合分けにはcond、またはifを使う。
条件は基本的に出てきた順で評価される。

問題1.1

10

→10

(+ 5 3 4)

→12

(- 9 1)

→8

(/ 6 2)

→3

(+ (* 2 4) (- 4 6))

→6

(define a 3)

→a

(define b (+ a 1))

→b

(+ a b (* a b))

→19

(= a b)

→#f

(if (and (> b a) (< b (* a b)))
    b
    a)

→4

(cond ((= a 4) 6)
      ((= b 4) (+ 6 7 a))
      (else 25))

→16

(+ 2 (if (> b a) b a))

→6

(* (cond ((> a b) a)
         ((< a b) b)
         (else -1))
   (+ a 1))

→16

問題1.2
次の式を前置記法に翻訳せよ.

→

(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5))))) (* 3 (- 6 2) (- 2 7)))

問題1.3
三つの数を引数としてとり, 大きい二つの数の二乗の和を返す手続きを定義せよ.
→

(define (square x) (* x x))
(define (sum-of-two x y) (+ (square x) (square y)))
(define (sum-of-biggers x y z) 
  (cond ((and (< x y) (< x z)) (sum-of-two y z)) 
            ((and (< y x) (< y z)) (sum-of-two x z)) 
            (else (sum-of-two x y))
  )
)

問題1.4
→
• 数字列の値は, その表す数値とする.
• 基本演算子の値は, 対応する演算を実行する機械命令の列とする.
• それ以外の名前の値は, その環境で名前と対応づけられたオブジェクトとする.
が基本的な式の扱いである。
そのため、帰結部が基本演算子の場合であっても、解釈系は基本演算子そのものを返す。

(define (a-plus-abs-b a b)
  ((if (> b 0) + -) a b))

この式は、b>0のとき(+ a b)をbodyとし、それ以外の時は(- a b)をbodyとした合成手続きを返す。

問題1.5
→
作用的順序の場合：
(test 0 (p))
ここで、testの本体を取り出す
(if (= x 0)
0
y))
次に、仮パラメタを引数で置き換える
(if (= 0 0)
0
(p)))
このとき、yの代わりに(p)を置き換えようとしている。
しかし、この(p)を評価したとき、pは自身を返すため、無限ループに陥る。

正規順序の場合：
(test 0 (p))
ここで、testの本体を取り出す
(if (= x 0)
0
y))
次に、仮パラメタを引数で置き換える。ただしこの時、まだ基本演算子を持つ式のみとなっていないので、引数の評価を行わない。
(if (= 0 0)
0
(p)))
if式の評価を行う。(= 0 0)が真なため、0が返される。